1.位权的理解 #
位权的定义：对于多位数 ，处在某一位上的“1”所表示数值的大小，称为该位的位权。 这句话怎么理解呢？我们可以这个来描述，从字面上来看，位权表示的是位置的权利。
以10进制为例： 个位的权利是把个位上所有的数都乘以1，所以他的位权是1，也就是100=1， 十位的权利是把十位上的数都乘以10，也就是101=10，所以它的位权就是10， 百位的权利是把百位上的数都乘以100，也就是102=100，所以它的位权就是100， ……….
如果我们把个位、十位、百位……都当成一个职位，那么这个职位的作用就是把职位上的数字根据个位、十位、百位……的位置不同而乘以100,101，102 ………，这个乘的系数就是位权。
从上面的描述来看，位权其实就是数位的意思，只是在计算机体系中换了个表达方式。 从十进制可以推广到二进制、八进制、十六进制上。
| 数制 | 基数 | 进位规则 | 位权 | 数码 | 表示 |
|---|---|---|---|---|---|
| 十进制 | 10 | 逢十进一 | 10i-1 | 0，1，2，3，4，5，6，7，8，9 | D |
| 二进制 | 2 | 逢二进一 | 2i-1 | 0，1 | B |
| 八进制 | 8 | 逢八进一 | 8i-1 | 0，1，2，3，4，5，6，7 | O |
| 十六进制 | 16 | 逢十六进一 | 16i-1 | 0，1，2，…，8，9，A，B，C，D，E，F | H |
按位权展开和进制转换：
十进制：123456.123=1×105+2×104+3×103+4×102+5×101+6×100+1×10-1+2×10-2+3×10-3
2.进制转换 #
转换规则表：
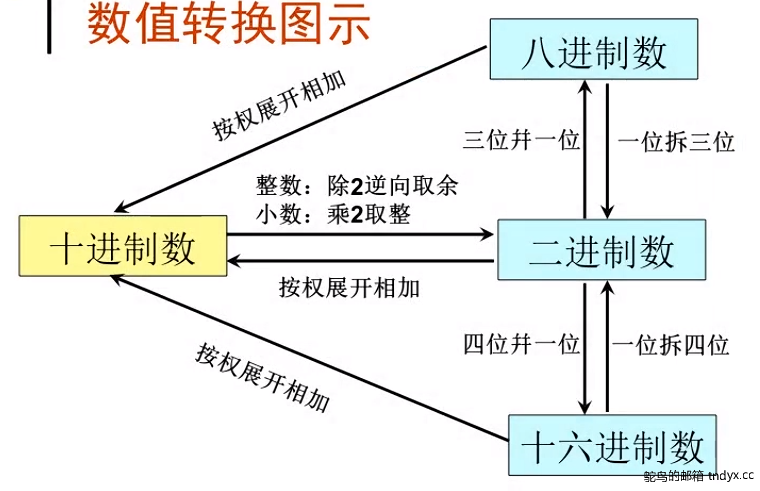下面举一些例子：
2.1 二进制转化为十进制： #
二进制：(10110.1)2(或者写作:10110.1B)=1×24+0×23+1×22+1×21+0×20+1×2-1 其他进制转化为十进制方法以此类推。
2.2 整数十进制转化为二进制：用除2取余法： #
2.3 小数十进制转化为二进制：乘2取整法： #
2.4 2进制到16进制和8进制的相互转换： #
